Retrospective biodosimetry: Conversion of frequency of chromosomal translocations into organ doses

INTRODUCTION

In cases of radiation exposure when a dosimeter was not available at the time of radiation exposure, retrospective biodosimetry can be used to reconstruct the radiation dose. One of the available biodosimetry approaches is based on the accounting of stable chromosomal aberrations (translocations) in human peripheral blood T-lymphocytes [1–3]. The application of this method is based on the following assumptions: the frequency of chromosomal translocations in T-lymphocytes is proportional to the exposure dose; the frequency remains constant for a long time (does not decrease with time); the radiation dose received by T-lymphocytes resulting in the formation of translocations corresponds to the dose of exposure to other organs and tissues, in particular to red bone marrow (RBM). The latter postulate is true in the case of uniform external or internal exposure. However, in case of non-uniform internal irradiation, for example, due to ^89,90Sr, when doses to the RBM and other organs may differ by an order of magnitude, difficulties arise when interpreting the results of cytogenetic methods. This problem has been discussed in detail in a number of reviews [1–2]. For the purposes of biodosimetry, a model of T-lymphocyte exposure was developed in the case of ^89,90Sr accumulation in mineralized tissues of the human body [4–6].

The fluorescence in situ hybridization (FISH) method is used to estimate the frequency of translocations in the cell. The main parameters required for retrospective dose estimation using FISH in case of internal non-uniform and prolonged β-irradiation are as follows.

(1) The number of y_i translocations in n_cell, counted in T-lymphocytes of a subject or a group of subjects is estimated using the FISH method. The characteristics of application and requirements for unification of the method are described in a number of regulatory documents [1][7]. To estimate the dose level, the translocation frequency (μ_i) is used; this should be presented per one genomic equivalent (Genomic Equivalent GE) — or, according to an alternative terminology, per one cell equivalent (Cell Equivalent CE). The conversion factor (G_j ) from the number of counted cells (metaphases) n_cell to the number of genomic equivalents n_ge depends on the set of stained chromosomes and the type of staining (single-color or multicolor). If 24-color staining is used, no conversion to GE is required.

(2) Background (non-radiation) translocation frequency μ₀(τ) depending on age. Here, since translocations may occur under the influence of other (non-radiation) unfavorable endogenous and exogenous factors, correction for background values (subtraction of background values) is necessary. The number of translocations in T-lymphocytes accumulates with age over an individual’s lifetime. According to the scientific literature, sex does not have a significant effect on the formation of translocations; the influence of smoking and alcohol is also insignificant. The dependence of translocation frequency obtained in a joint international study of unexposed donors in terms of the number of translocations per GE is used as already known background values [8].

(3) Coefficients of the dose-effect relationship (C — free term, α — linear coefficient, β — quadratic coefficient), whose combination permits age-adjusted translocation frequency μ_{i_age} to be transposed onto the dose absorbed in T-lymphocytes (D_L). The coefficients are determined on the basis of the calibration curve (linear-quadratic or linear). For the construction of the calibration curve, the reliability of radiation dose estimation and uniformity of translocation counting criteria are of fundamental importance. The shape and parameters of the calibration curve depend on the type of radiation (linear energy transfer LET); sparsely ionizing gamma and beta radiation are dependent on the dose rate. Calibration curves are discussed in detail in the literature [1][7][9].

(4) Conversion factor (B_rbm) from lymphocyte dose (D_L) to red bone marrow dose (D_rbm). For osteotropic ^89,90Sr, this coefficient depends on age at the time of irradiation onset (τ₁) and time following irradiation onset (τ_s – τ₁), where τ_s is the age of the donor at the time of blood collection. In addition, the coefficient depends on sex due to variable strontium metabolism and its accumulation in bone tissue [10].

The purpose of this analytical review is to consider the main parameters¹ that are necessary for retrospective dose estimation using the FISH method in the case of internal nonuniform and prolonged β-irradiation.

FINDINGS

Chromosome translocations taken into consideration under retrospective biodosimetry

For good reproducibility of the biodosimetry method, it is important to unambiguously define the types of chromosomal translocations that are considered. Radiation cytogenetics uses different nomenclature approaches, typically PAINT (Protocol for Aberration Identification Nomenclature Terminology) [11], S&S (Savage and Simpson) [12]), and a combined approach using International System for Human Cytogenomic Nomenclature (ISCN) medical genetics terminology [13]. In the Russian-language literature, this leads to a large number of synonyms for translocations.

Under the action of sparsely ionizing β-radiation characteristic of ^89,90Sr, most of the registered translocations are reciprocal (synonyms: complete, bilateral, two-way). In this case, there is a mutual exchange of end sites between two non-homologous chromosomes without loss of genetic material. Despite the involvement of fact that two chromosomes, reciprocal translocation is considered as a single event, i.e., one translocation. A small proportion are nonreciprocal (incomplete, unilateral, one-way) translocations, when the transfer of material occurs only from one nonhomologous chromosome to another — i.e., unidirectionally — and is counted as a single event. It has been suggested [1][14][15] that an incomplete translocation may actually be complete, but that the second chromosome segment involved in the exchange is too small to visualize. Reciprocal and nonreciprocal (complete and incomplete) translocations are also referred to as simple translocations. Here, the main indicator on the basis of which the radiation dose is calculated when using the FISH method is their frequency.

Complex translocations, when three or more chromosomes are involved in the exchange, make up a small fraction of the total number of translocations under prolonged sparsely ionizing radiation [16][14]. Difficulties can arise due to counting complex translocations as the sum of simple translocations, whose number is determined by the number of color transitions [17]. Under conditions of densely ionizing radiation, the proportion of complex translocations increases significantly [18][19].

In the publication of the International Atomic Energy Agency, 2011 [1], chromosomal translocations also include insertions in cases when a visible insertion of a region of one chromosome into the arm of a nonhomologous chromosome is observed. The authors note that the frequency of insertions may or may not be taken into account when estimating the radiation dose.

Cytogenetic analysis may also take into account inversions representing intrachromosomal aberrations in which there is a 180° reversal of a chromosome segment. Indication of inversions requires more complex staining — for example, by Multicolor Banding Probes (mBAND) or by combining whole chromosome probes together with telomeric probes. The frequency of inversions is significantly increased by exposure to densely ionizing radiation [18][19].

If several lymphocytes contain identical translocations (the numbers of chromosomes involved in the exchange and the length of the translocated sites are the same), such cells are considered to be clones [1]. In this case, it is assumed that a single translocation occurred in one cell regardless of the number of cells with identical translocations.

Estimation of the frequency of chromosomal translocations for the purposes of retrospective biodosimetry is usually performed in so-called stable cells, i.e., cells that do not contain unstable chromosomal aberrations such as rings and dicentrics that prevent normal cell cycle progression. Unstable cells contain the aberrations mentioned above.

CONVERSION FACTORS FROM THE FREQUENCY OF RADIATION-INDUCED TRANSLOCATIONS TO THE DOSE TO T-LYMPHOCYTES

General approaches

The description of dose-effect relationships for translocation frequency are described in detail in the literature along with approaches to parameter determination [1][7][9][13][20]. In our case, the dependences for sparsely ionizing radiation are of interest.

Numerous experiments have demonstrated a linear-quadratic dependence of the frequency of radiation-induced translocations (μ_i) of lymphocyte radiation dose D_L at high dose rates (irradiation time less than 2 hours):

μ_i = C + α ∙ D_L + β ∙ D_L², (1)

where:

С — absolute term of the dose-effect relationship;

α — linear dose-effect coefficient;

β — quadratic coefficient of the dose-effect relationship.

Such a dependence can be explained as follows. It is assumed that the quadratic term β takes into account DNA damage (the source of translocation formation Tr) arising from repeated hits of ionizing particles into the cell nucleus with a short time interval (<2 h). In other words, the coefficient β takes into account aberrations that can be altered by repair mechanisms if they manage to “work” during prolonged exposure or in periods between intermittent (fractionated) acute exposures. Most lesions resulting in chromosomal aberrations are either repaired or become unavailable for repair within about five to six hours after exposure. Therefore, an additional coefficient is proposed for the quadratic term in the form of a G-function [1][21][22], which takes into account the time required for damage repair, i.e., the dose rate:

μ_i = C + α ∙ D_L + β ∙ G(x) ∙ D_L², (2)

G(x) = 2/x² ∙ [x – 1 + e^–x], (3)

in this case, x = t / t₀, (4)

where:

t — time (duration) of irradiation,

t₀ — average rupture lifetime, which has been shown to be about 2 hours.

When a dose accumulates over a long period of time, G(x) decreases about to zero. Consequently, even if prolonged irradiation occurs with a high dose (>1.0 Gy), the dose dependence of the translocation frequency becomes linear:

μ_i = C + α ∙ D_L. (5)

It is also evident that most aberrations due to the action of sparsely ionizing radiation at low doses (<0.3 Gy) but with high power occur during the passage of single ionizing tracks, resulting in a dependence close to linear.

Thus, a dependence close to linear is observed when there is has been prolonged irradiation (duration of irradiation was days, months, years), including with high accumulated doses (up to 2–3 Gy), or in the case of acute irradiation with low doses when no acute radiation syndrome was detected. Therefore, for retrospective assessment of doses in cases of internal exposure to ^89,90Sr, the estimation of the linear coefficient α is of fundamental importance.

As the analysis of experimental data [1] shows, the linear coefficient in formula 5 will be the same both when studying the dose dependence of the translocation frequency and when analyzing the dose dependence of the yield of unstable aberrations (dicentrics, rings). As noted in [23][24], the ratio of dicentrics to radiation-induced translocations is approximately 1:1; as a result, similar ratios in the dose-effect relationship can be expected. According to the dicentrics data, the linear coefficient for translocations for high-energy gamma rays in the case of uniform prolonged irradiation is 0.015–0.020 Tr/GE per Gy [25], which can be used to convert from translocation frequency to dose to lymphocytes. In [26], the recommended value is ~0.015.

Thus, based on (5) and taking into account the background values for the corresponding age (μ₀(τ_s)), the dose to T-lymphocytes is obtained using the formula:

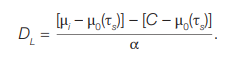 (6)

Since the absolute term C is mainly due to the background translocation frequency, the expression [С – μ₀(τ_s)] is assumed to be close to zero, so:

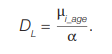 (7)

Approaches to estimating the coefficients of α are discussed below.

Estimates of the parameter α obtained by acute external gamma irradiation of donor lymphocytes in vitro

Recently, a number of studies have appeared aimed at obtaining calibration curves for translocations estimated by the FISH method under the condition of standardization [1][9][20], which assumes acute irradiation, application of a linear-quadratic model, standard statistical approaches, etc. In order to use the parameters of these dependencies for retrospective dosimetry, translocations must be calculated in stable cells where there are no unstable aberrations interfering with the cell cycle. Since at prolonged irradiation the dose dependence of translocation yield is close to linear, the linear coefficient α should be considered from the obtained parameters of the linear-quadratic dependence for the transition from the translocation frequency to the dose to lymphocytes.

The article [9] gives an overview of the parameters of calibration curves for translocations (determination of coefficients α and β of the linear-quadratic dependence) obtained by FISH following subtraction of background values. As well as being sporadic, such works also differ in their approaches to accounting for translocations (Tr). Table 1 summarizes the results of the most appropriate cytogenetic studies where the α coefficient was statistically significantly determined by in vitro lymphocyte irradiation. In all cases, the authors irradiated donor blood from a ⁶⁰Co source with a high dose rate; the irradiation time was measured in minutes and the dose-effect was described by a linear-quadratic relationship (formula 1). Table 1 shows that the variation of α values is significant (from 0.012 to 0.0447); the median value is equal to 0.0178 (95% 0.012-0.044) Tr/GE per Gy.

Evaluation of α parameter used in irradiation process in vivo

For in vivo irradiation, the dose to T-lymphocytes and other organs is calculated on the basis of dosimetric measurements. In this case, dose measurements are not made directly in the target cells or tissues, but either by means of a dosimeter located close to the body (in professionals) or by measuring the radionuclide content in the body in the population (measurement of ⁹⁰Sr content in the bodies of residents of coastal villages of the Techa River), or by reconstructing gamma fields and radiation spectra as in the case of the nuclear bombings of Hiroshima and Nagasaki.

Acute external irradiation of complex spectrum with high power (Hiroshima and Nagasaki populations)

In the cases of atomic bombing, there was an acute single exposure of the population with high dose rate and different LET. Therefore, in order to analyze the dose dependence it is necessary to introduce coefficients that take into account the relative biological effectiveness (RBE) of radiation, which introduces additional uncertainty in dose estimates. In addition, it is known that densely ionizing radiation leads to a large number of complex (compound) damages of DNA and chromosomes [18][19]. This makes it difficult to directly use these data for cases of sparsely ionizing radiation. On the other hand, the cohort of those exposed due to atomic bombardments is the most studied, so the results of cytogenetic studies deserve attention. Dose-dependent analysis of the frequency of stable chromosomal aberrations for the residents of Hiroshima and Nagasaki has been conducted since the 1960s. The results were published as cytogenetic data accumulated and/or as the system for calculating individual doses improved [31–34]. The analysis of cytogenetic data of key interest to us (but using routine Gimza staining of chromosomes) was performed in [34], where reciprocal translocations, pericentric inversions, or small deletions (or their combinations) were considered as stable. Translocations in stable cells — i.e., cells without dicentrics and rings — were counted. The dose-effect relationship was described by a linear-quadratic function (Formula 1). A total of 1703 individuals were included in the study. Individual equivalent doses were calculated with correction for the RBE of neutrons and γ-radiation. The maximum individual doses were 1.5 Sv. The following values of the linear coefficient were obtained:

For Hiroshima inhabitants α = 0.03915 ± 0.00315 Tr to the cell per Zv

μ_i = (0.01274 ± 0.01399) + (0.03915 ± 0.00315) D_L + (0.00970 ± 0.00155) D_L².

For Nagasaki inhabitants α = 0.02350 ± 0.00246 Tr to the cell on Zv

μ_i = (0.01274 ± 0.11399) + (0.02350 ± 0.00246) D_L + (0.01870 ± 0.00099) D_L².

In general, these values are higher than those obtained for the calibration curves (Table 1), but fall within the range of scatter of their values.

The last analysis of the data obtained using FISH and the updated version of the dosimetry system was performed in [35]. Reciprocal and nonreciprocal translocations, insertions (insertions), and complex exchanges were taken into account. The excess relative rate (ERR) of translocation frequency was calculated with correction for background. Although dose-effect parameters for ERR cannot be directly used for quantitative comparison with literature data, the authors noted interesting patterns. Linear-quadratic dependence of translocation frequency (in terms of ERR) on dose was observed up to 1.25 Gy. Thus, the dependence had a more complex character. It was shown that age at the time of irradiation is a significant factor affecting the dose-effect parameters. The lowest values of translocation frequency per 1 Gy were observed in the group of children aged 0–5 years, then the frequency increased to decrease again after 25 years of age.

Prolonged external γ-irradiation with low dose rate (professionals)

The analysis was performed as described in [36]; male workers (n = 459) were included in the study; the dose was up to 1.6 Gy (the accumulated dose was determined on the basis of individual dosimeter data as the dose per RBM). Using the FISH method, simple Tr translocations in stable cells per GE were counted. Data were described by linear regression (Poisson distribution of translocation frequency was tested for each dose group). The AMFIT module of the EPICUR program was used for calculations: α = 0.01174 ± 0.00164.

These values fall within the lower limit of the interval of estimates of the α coefficient from the in vitro calibration curves.

Prolonged external and internal exposure of residents of riverside villages of the Techa River (Southern Urals) with decreasing dose rate

The inhabitants of the riverside villages of the Techa river suffered from radiation expose (mixed γ-, β-irradiation with low dose rates, both external and internal) following discharges of radioactive waste from the Mayak Production Association into the Techa River during the 1950s. External exposure was more pronounced in the upper reaches of the Techa River near to site of radioactive waste discharges. However, throughout the river, the main contribution to the internal dose to the RBM was made by ^89,90Sr. Dose-response analysis was performed in 2023 and described in detail [37]. We used pooled data for a long period of studies from 1994 to 2021 (197 donors, 212 blood samples). For each donor, the dose to T-lymphocytes was calculated taking into account age-related dynamics and kinetics of T-cell populations. Simple translocations and complex exchanges in stable cells were taken into account. As in the above-mentioned study [33], the dose dependence of translocation frequency was described by linear regression (Poisson distribution of translocation frequency was checked for each dose group); the AMFIT module of the EPICUR program was used for calculations.

Table 2 shows the values of linear coefficients of α-dose-effect dependence for donors of different ages at the time of the beginning of irradiation in 1950.

The lowest values of translocation frequency per 1 Gy dose to T-lymphocytes were obtained for children of the first years of life (Table 2). The maximum values were observed in the group from 5 to 18 years of age. The data of Table 2 do not contradict the results obtained in vitro (Table 1) and in vivo for professionals [36]. It should be noted that these data are consistent with the results on the evaluation of the effect of age at the time of irradiation on the translocation rate in the Japanese cohort [35], where relatively low values of ERR per 1 Gy were observed in children of the first years of life, followed by an increase in the translocation rate and subsequent decrease in adults after 25 years of age.

To summarize, the in vitro calibration curves described in the literature were obtained by irradiating blood samples with high dose rates (irradiation lasting minutes). Adults aged 25 to 45 years were taken as donors.

The number of donors for the construction of one calibration curve is small (a maximum of 11 people [7], of which sharply falling out values were obtained for two donors, who differed from the rest of the group by almost 10 times. The International Organization for Standardization (ISO) [7] recommends that biodosimetry laboratories develop their own calibration curves to take into account the staining and translocation counting methods adopted by the laboratory and the age range of the subjects. Examples of such work include [20][30].

Although estimates obtained in vivo are based on the study of a large number of donors, the accuracy of dose estimates is much lower. In these studies, parameter values may change with improvements in dosimetric approaches, as is done in the Japanese cohort studies and the Techa River studies.

CONVERSION FACTORS FROM THE DOSE TO T-LYMPHOCYTES (CYTOGENETIC DOSE) TO THE DOSE TO CRITICAL ORGANS AND TISSUES

In the case of uneven internal irradiation, the dose to T lymphocytes is not the same as the dose to other organs and tissues, of which the dose to RBM is of most interest. Coefficient (B_org) can be used to relate the dose to lymphocytes (D_L) to the dose on the body (D_org). Thus, taking into account formula (7), the dose to a particular organ based on cytogenetic data will be calculated according to the formula:

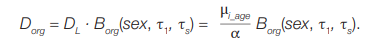 (8)

Dose shaping to different T-cell populations during prolonged internal non-uniform irradiation (on the example of ⁹⁰Sr)

If the irradiation occurred decades ago, the donor’s blood contains a mixture of T-lymphocytes, which are descendants of T-cells irradiated at different doses. Two groups of T-lymphocytes can be distinguished, the dose to which differs most significantly in the case of local irradiation of RBM ⁹⁰Sr.

(1) T-lymphocytes are the descendants of lymphocytes formed (emerged from the thymus) before exposure. Their proportion can be quite significant if the exposure occurred during adolescence and adulthood. Despite the fact that the lifespan of individual lymphocytes is several years (varies in different subpopulations) [38-40], T-lymphocytes are able to proliferate in peripheral lymphoid organs, maintaining quantitative constancy of the peripheral pool of T-cells [41–42] against the background of a sharp age-related decrease in thymus production [39][40][43]. These T-lymphocytes are irradiated only when circulating in the body, spending a certain time, including the bone marrow.

(2) T-lymphocytes, progenitors of progenitors (stem cells) irradiated in the RBM after ⁹⁰Sr enters the body. The dose load on these cells is much higher than on T-lymphocytes from the first group due to the accumulation of ⁹⁰Sr in bone tissue to locally irradiate RBM, including T-progenitors. After passing through the stages of differentiation and proliferation in the RBM and in the thymus, the formed T-lymphocytes continue to circulate and in some cases proliferate in the body; their descendants may appear in the donor’s blood sample decades after the beginning of irradiation.

The works [4][6][37][44] describe in detail approaches to modeling the dynamics and biokinetics of T cells based on the concept of T-cell lineage, when the modeling unit is the progenitor and all its progeny (potential carriers of stable aberration). Modeling approaches can be used to determine weighting coefficients for these two groups of T-lymphocytes and estimate the weighted average dose per T-lymphocyte. The evaluations rely on dose calculations to the RBM and other organs and tissues based on dosimetric and biokinetic models for ⁹⁰Sr [45–46].

Evaluation of transition factors from dose to T-lymphocytes (D_L) to dose to critical organs using ⁹⁰Sr as an example

The estimation of the conversion factors from dose to T lymphocytes to dose to critical organs (B_org) using ⁹⁰Sr as an example was described earlier [10]. This factor is the ratio of the corresponding dose coefficients — i.e., the values of the accumulated dose in the case of a single intake of the radionuclide. For a single intake, the following formula is used:

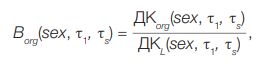 (9)

where:

τ₁ — the age of the donor at the moment of ⁹⁰Sr intake (years)

τ_s — the age of the donor at the time of blood collection for FISH cytogenetic study

Dc_org(sex, τ₁, τ_s) — the dose accumulated in the organ org during the period of time (τ_s – τ₁) after a single intake with food 1 Bq ⁹⁰Sr; is calculated using dosimetric [45] and biokinetic models [46] that take into account the sex and age of the individual;

Dc_L(sex, τ₁, τ_s) — weighted average dose accumulated over a period of time (τ_s – τ₁) in a series of T-cell generations after a single food intake of 1Bq ⁹⁰Sr; calculated using the model of age dynamics and T-cell kinetics, as well as known values of D_org doses for organs and tissues in which T-cells spend some time [47]; Gy/Bq. The computer program “Lymphocytes” was used for calculations. Numerical values Dc_org(sex, τ₁, τ_s) for ⁹⁰Sr are shown in the study [47]. In the case of chronic ingestion, the sum of the dose values from activity ingestion was calculated A_i(t) in every marked period of time. Therefore, for B_org we consider the following:

 (10)

Since the values of A_i(t) in the numerator and denominator of formula (10) are reduced in the case of uniform arrival:

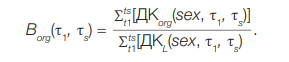 (11)

However, if the chronic intake was uneven (function A_i(t) is not constant), coefficient B_org must be calculated considering this function.

Numerical values of coefficients B_org, which connect the dose on T-lymphocytes and dose to RBM, were counted and analyzed for ^89,90Sr (B^Sr_rbm), [10]. Coefficients B^Sr_rbm turned out to significantly depend on the age at the beginning of ^89,90Sr intake. The older a person is at the beginning of exposure, the more the cytogenetic dose differs from the dose to the RBM because the coefficient B^Sr_rbm is growing with age and can and may exceed the value of 5.

This is due to the age-related dynamics of T-cell populations: it is only legitimate to assume that the cytogenetic dose corresponds to the dose to RBM for newborns and children in the first years of life for whom the values of B^Sr_rbm are close to one.

Sex does not have a significant impact on B^Sr_rbm. If homogeneous enrollment was stretched in time by six months, it did not significantly affect the value of the B^Sr_rbm. The study of the effect of the longer intake of ⁹⁰Sr to B^Sr_rbm (up to 5 years) showed that the most sensitive group is adolescents of 15 years old. For this cohort, the differences of B^Sr_rbm in the case of a single and 5-year even ⁹⁰Sr intake are about 13%.

UNCERTAINTY OF DOSE ESTIMATES IN RETROSPECTIVE BIODOSIMETRY, RESEARCH DIRECTIONS

In the case of acute whole-body gamma irradiation, the approaches to dose estimation uncertainty are described in detail in [7]. The uncertainties of all input parameters are taken into account: the uncertainty of the translocation frequency estimate, the uncertainty of the calibration curve, and the uncertainty of the age-specific background translocation frequency estimate. These approaches allow estimating the limits of the 95% confidence interval (CI) of the radiation dose to T-lymphocytes, which differs little from the dose to RBM and other organs and tissues. The simplest method [48] is based on estimating the lower and upper limits of CI for the frequency of chromosomal aberrations (in the Poisson distribution approximation) and comparing them with the CI of the calibration curve. In this case, the CI width for the frequency of chromosomal aberrations is chosen to be 83%, which gives 95% CI for the transition to dose uncertainty estimation [49].

More complicated is the method of uncertainty propagation or delta method [1][7], which is based on estimates of the variation (and covariance) of the calibration curve parameters and aberration frequency variance in terms of standard deviation. In this case, the 95% CI of the dose estimate is calculated in the approximation of a normal distribution. This is a conservative method used, for example, for “alien” calibration curves. The need to switch from dose to T-lymphocytes to dose to other organs and tissues is relevant for non-uniform external and internal irradiation.

For the case of non-uniform (partial) external irradiation, scenarios of local irradiation of different segments of the human body containing RBM (e.g., sternum, pelvis, head, etc.) are considered. However, all the proposed statistical methods for estimating the dose accumulated by tissues in the irradiated area (with an estimate of their uncertainty) are based on dicentrics analysis, i.e., they should be applied in a short period of time after exposure [1][50]. The methods are based on the use of the “contaminated” Poisson method, which allows dose estimation to take into account the distribution of dicentrics among all affected cells, as well as providing additional information about the irradiated body volume and RBM. The above methods — in particular, using the Bayesian approach [51] — are implemented in the BiodoseTool, DoseEstimate, and CABAS [50–53] computer programs. However, the applicability of these statistical methods for retrospective dosimetry of internal exposure (using the translocation frequency) is highly questionable, since, as noted above, by the time of blood sampling, different subpopulations of lymphocytes have accumulated different doses depending on the age of the donor at the time of 90Sr intake making it impossible to divide the Poisson distribution into two components.

Under uneven inner irradiation as in the case with ⁹⁰Sr, the total uncertainty should include — but not be limited to — the uncertainty of factor estimates B_org (Formula 11). Approaches to its assessment currently being developed represent one of the most important directions of our work. It should be noted that individual donor differences in the ability to repair DNA damage (individual differences in the efficiency of repair enzymes) — as well as donor lifestyle, which determines the occurrence of other endogenous and exogenous factors that influence the background frequency of translocations — contribute to the uncertainty of dose estimates.

The total uncertainty determines the threshold of individual doses that can be detected using the FISH method (minimum detectable value). A review by Edwards et al. [26] indicates that supra-phononuclear individual doses of the order of 0.5 Gy can be measured using FISH. In general, reviews on the application of retrospective dosimetry methods note a detectable individual dose value of 0.25–0.3 Gy [54-57] or 0.25–0.4 Gy [3]. In the case of internal ⁹⁰Sr exposure, this value can be expected to be higher.

For the purposes of retrospective dosimetry, not only individual but also mean group dose estimates using the FISH method are in demand. Such assessments are used in the case of radiation accidents in which large populations are affected or where there is a need to estimate average doses in a locality with a conditionally uniform level of contamination/exposure. In this mean group approach, the total number of translocations detected in all donors in the group is summarized along with the number of background translocations according to the age of each donor in the group. The difference between these numbers considered as radiation-induced translocations refers to the total number of genome-equivalents calculated in the group. Such an approach avoids the null and negative values that often occur when background is subtracted at the individual level at low radiation doses, thus significantly lowering the threshold for detecting dose exceeding the background values. However, the mean group approach requires careful formation of groups with maximally similar exposure conditions. Mean group estimates can also be used to validate individualized dose estimates derived from models and/or other retrospective dosimetry techniques, which include:

• reconstructing external dose to human organs and tissues from soil contamination levels (includes calculations using human body phantoms);
• reconstructing internal doses from dietary contamination (includes the use of dosimetric and biokinetic models);
• using other biodosimetry techniques such as electron paramagnetic resonance (EPR) method for tooth enamel;
• dosimetry using materials sensitive to ionizing radiation (e.g., thermoluminescent dosimetry using ceramic samples).

The use of cytogenetic data for the purposes of validation of external doses is exemplified in the studies on the Techa River [58][59], where good convergence of the results of estimation of doses to members of epidemiological cohorts estimated on the basis of direct measurements of gamma fields, human body exposure models, data from cytogenetic FISH studies, studies of tooth enamel by the EPR method, etc., was shown.

CONCLUSION

The used of translocation frequency to provide dose estimates is challenging especially in cases of non-uniform internal irradiation with low dose rates. The conversion factors from chromosomal translocation frequency to T-lymphocyte dose (α) and further from T-lymphocyte dose to organ and tissue dose B_org, which are determined from independent data sets, rely on different approaches.

The α coefficient requires experimental characterization of the calibration curves, since its estimates vary widely, often differing by a factor of two; in addition, values depend on the specific FISH technique used. Calibration curves obtained in vitro for children and adolescents at the time of exposure, whose parameters may differ from those for adults, are not described. No in vitro calibration curves are available for prolonged irradiation at low dose rates. Due to the small number of donors, the curves may involve systematic bias in the dose-effect parameters.

The estimation of the B_org coefficient relies on a set of models, which, in turn, are based on a large amount of experimental data on human physiology, mineral metabolism, anatomical structure of organs, etc. The coefficients depend significantly on age at the time of exposure. Unfortunately, approaches to estimating their uncertainties remain undeveloped to date.